4.3 Teorema de Bernoulli para fluidos perfeitos
Resulta da aplicação do princípio da conservação da energia. No escoamento permanente de um fluido perfeito, a soma das alturas piezométricas (\(P/\gamma\)), cinética (\(V^2/2g\)) e geométrica (\(z\)) ao longo da linha de corrente se mantém constante (Eq. (4.4)).
\[\begin{equation} \frac{P_1}{\gamma} + \frac{V_1^2}{2g} + z_1 = \frac{P_2}{\gamma} + \frac{V_2^2}{2g} + z_2 = constante \tag{4.4} \end{equation}\]
- Energia de pressão (\(P/\gamma\)): representa a quantidade de trabalho necessária à movimentação do fluido contra a pressão reinante no sistema.
- Energia cinética (\(V^2/2g\)): está associada a velocidade de escoamento do fluido no conduto.
- Energia gravitacional (\(z\)): está associada a posição da massa em relação a um referencial de posição.
Todas as unidades deverão ser expressas em pressão em termos de altura de fluido (mca).
Exemplo 4.5 (Bernoulli) Uma tubulação é constituída de dois trechos (1 e 2) com 200 mm e 250 mm, respectivamente. A altura do ponto 1 em relação ao referencial é de 10 m, e do ponto 2 é de 20 m. Sabendo que a pressão manométrica no ponto 1 é de 1,5 kgf/cm2 e que a velocidade da água neste mesmo ponto é de 0,6 m/s, calcule a pressão no ponto 2.
Solução.
\(P_1 = 1,5 \cdot \frac{10^3}{10^4} = 15 mca\)
\(V_2 = V_1 \cdot \frac{D_1^2}{D_2^2} = 0,6 \cdot \frac{200^2}{250^2} = 0,38 m/s\)
\(15 + \frac{0,6^2}{19,62} + 10 = P_2 + \frac{0,38^2}{19,62} + 20\)
\(P_2 = 5,0 mca\)
No vídeo abaixo tem a explicação mais detalhada.
Exemplo 4.6 (Vazão na mangueira) Sendo a altura h=3 m, qual a vazão na mangueira (20 mm de diâmetro)? Obs: desprezar as perdas de energia.
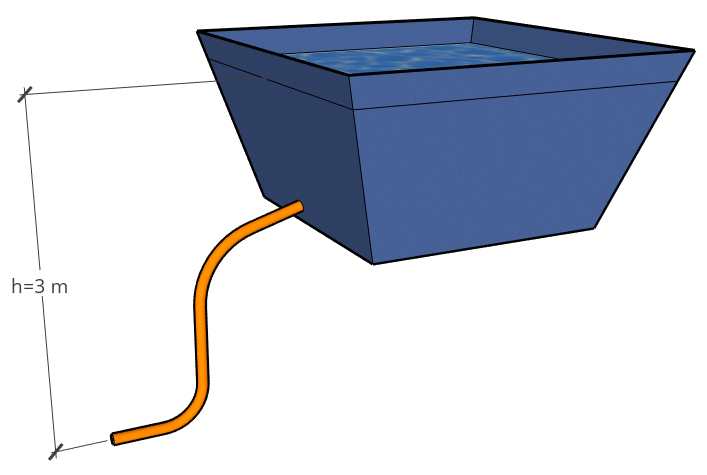
Solução.
\(\frac{P_1}{\gamma} + \frac{V_1^2}{2g} + z_1 = \frac{P_2}{\gamma} + \frac{V_2^2}{2g} + z_2\)
\(0 + 0 + 3 = 0 + \frac{V_m^2}{19,62} + 0\)
\(V_m = 7,76 m/s\)
\(Q = A \cdot V = \frac{\pi 0,020^2}{4} \cdot 7,67 = 0,0024 m^3/s = 2,4 L/s\)