6.2 Extensão do Teorema de Bernoulli aos casos práticos
A experiência não confirma rigorosamente o Teorema de Bernoulli, isto porque os fluidos reais se afastam do modelo perfeito. A viscosidade e o atrito são os principais responsáveis pela diferença, o escoamento somente ocorre com uma perda de energia: a perda de carga.
Por isso, se introduz na equação de Bernoulli um termo corretivo hf (perda de carga):
\[ \frac{P_1}{\gamma} + \frac{V_1^2}{2g} + z_1 = \frac{P_2}{\gamma} + \frac{V_2^2}{2g} + z_1 + hf_{1 \rightarrow 2} \]
O enunciado do Teorema de Bernoulli fica sendo, portanto:
Para um escoamento permanente, a carga total de energia em qualquer ponto de uma linha de corrente é igual a carga total em qualquer ponto a jusante da mesma linha de corrente somada a perda de carga entre os dois pontos.
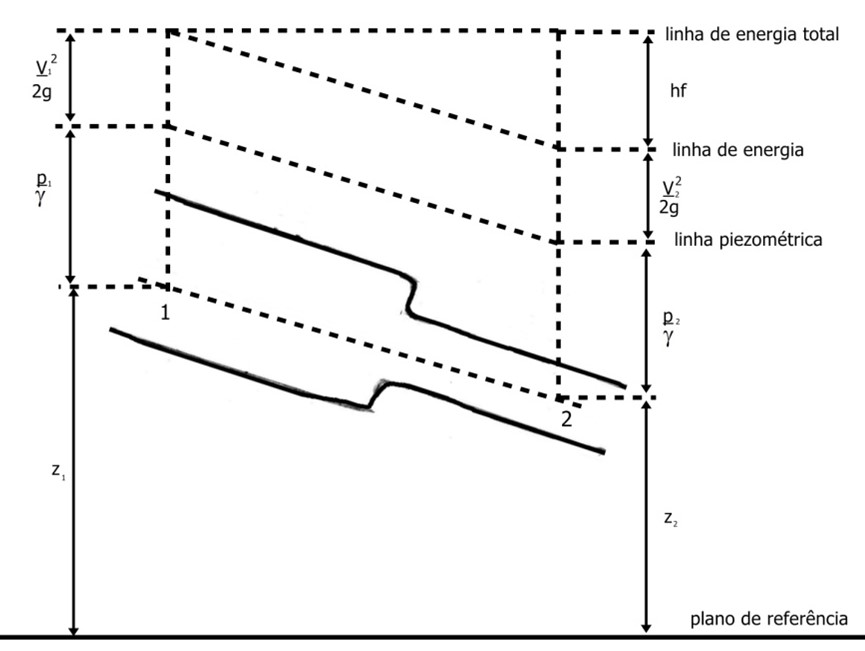
Figura 6.1: Representação do Teorema de Bernoulli aplicado a fluidos reais.
Na figura acima, podemos verificar:
- As distâncias dos pontos 1 e 2 ao plano de referência correspondem às cargas de posição z1 e z2.
- Marcando-se acima dos pontos 1 e 2 as respectivas cargas piezométricas (\(\frac{P}{\gamma}\)) fica definida a linha piezométrica
- A soma \(\frac{P}{\gamma} + z\) representa a energia potencial do fluido em relação ao referencial adotado
- Adicionando o termo cinético () se obtém a linha de energia do escoamento.
- A energia em 1 é maior que em 2 uma quantidade igual a perda de carga, energia dissipada irreversivelmente.
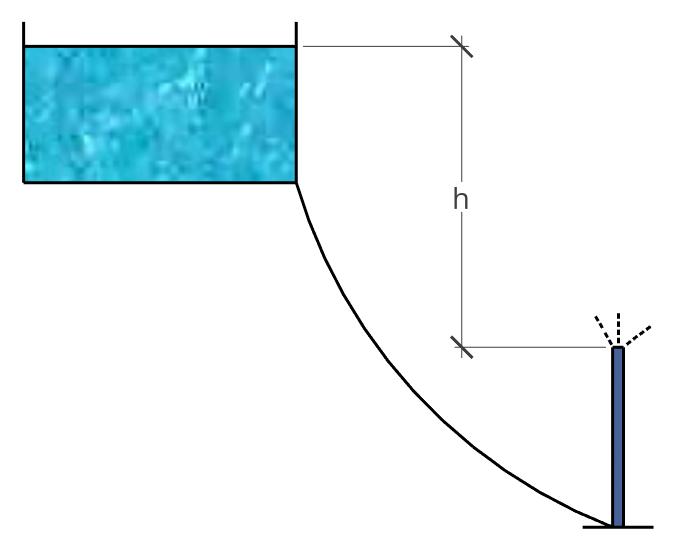
Exemplo 6.1 (Perda de carga 1) A água flui de um reservatório até um aspersor funcionando com uma vazão de 5 m3/h e uma pressão de serviço de 3 kgf/cm2. Tendo a tubulação um diâmetro de 25 mm, e a altura h=50 m, calcule a perda de carga (hf) entre A e B.
Solução.
Velocidade:
\(V_B = \frac{4 \cdot 5/3600}{\pi \cdot 0,025^2} = 2,83 m/s\)
Perda de carga:
\(0 + 0 + 50 = 30 + \frac{2,83^2}{19,62} + 0 + hf_{A \rightarrow B}\)
\(hf_{A \rightarrow B} = 19,6 mca\)
Exemplo 6.2 (Perda de carga 2) O diâmetro de uma tubulação aumenta gradualmente de 150 mm em B para 450 mm em A, estando o ponto A 4,5 m abaixo do ponto B. Se a pressão em A for de 0,7 kgf/cm2 e em B de 0,490 Kgf/cm2, e a descarga de 140 L/s, qual o sentido do escoamento e a perda por atrito entre os dois pontos?
Solução.
Velocidade:
\(V_A = \frac{4 \cdot 0,140}{\pi \cdot 0,450^2} = 0,88 m/s\)
\(V_B = \frac{4 \cdot 0,140}{\pi \cdot 0,150^2} = 7,92 m/s\)
Perda de carga:
\(7 + \frac{0,88^2}{19,62} + 0 = 4,9 + \frac{7,92^2}{19,62} + 4,5 + hf_{A \rightarrow B}\)
\(hf_{A \rightarrow B} = -5,56 mca\)
\(hf_{B \rightarrow A} = +5,56 mca\)
Sentido de B para A
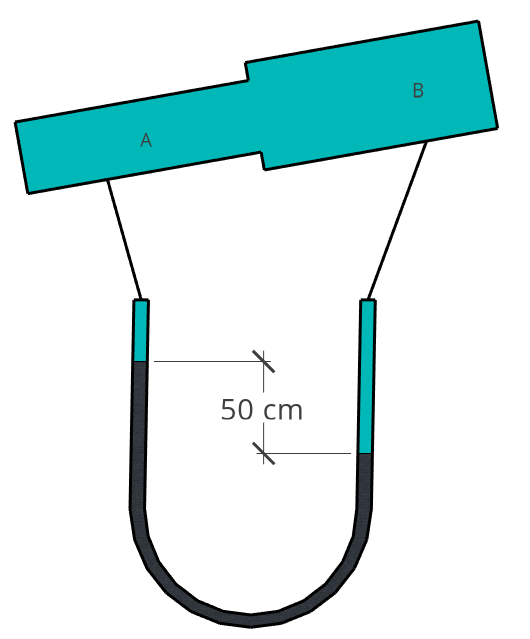
Exemplo 6.3 (Perda de carga 3) A canalização inclinada esquematizada na figura é composta por 2 trechos de diâmetro 50 mm e 75 mm cuja diferença de altura é 1,0 m. Analisando a deflexão da coluna de mercúrio do manômetro diferencial e sabendo que a canalização conduz água a uma vazão de 5 L/s, determine o sentido do escoamento e a perda de carga no trecho AB.
Solução.
Diferença de pressão:
\(P_A + 0,5 \cdot 13,6 = P_B + 0,5 \cdot 1 + 1\)
\(P_B - P_A = 5,3 mca\)
Admintindo uma pressão qualquer no ponto A, digamos, PA=0, então, PB=5,3 mca.
\(V_A = \frac{4 \cdot 0,005}{\pi \cdot 0,050^2} = 2,55 m/s\)
\(V_B = \frac{4 \cdot 0,005}{\pi \cdot 0,075^2} = 1,13 m/s\)
\(0 + \frac{2,55^2}{19,62} + 0 = 5,3 + \frac{1,13^2}{19,62} + 1 + hf_{A \rightarrow B}\)
\(hf_{A \rightarrow B} = -6,03 mca\)
\(hf_{B \rightarrow A} = +6,03 mca\)
Sentido de B para A
Neste vídeo está a solução detalhada desta série de exercícios: