6.4 Perda de carga localizada
A perda de carga localizada é aquela provocada pelas peças especiais e demais singularidades presentem em uma tubulação.
Há várias maneiras para efetuar seu cálculo, sendo uma das mais simples o métodos dos comprimentos virtuais.
Uma canalização que compreende diversas peças especiais e outras singularidades, sob o ponto de vista de perdas de carga, equivale a um encanamento retilíneo de comprimento maior. O método consiste em se adicionarem à extensão da canalização, para simples efeito de cálculo, comprimentos tais que correspondam à mesma perda de carga que causariam as peças especiais existentes na canalização. A cada peça especial corresponde um certo comprimento fictício e adicional. Levando-se em consideração todas as peças especiais e demais causas de perda, chega-se a um comprimento virtual de canalização.
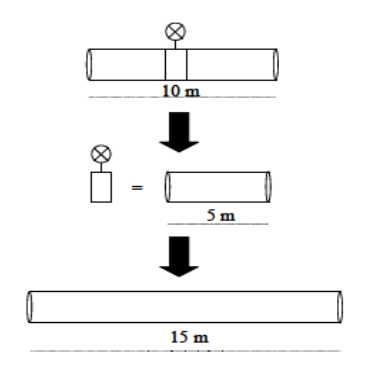
Figura 6.2: Representação da perda de carga localizada pelo método dos comprimentos virtuais.
Para a determinação dos comprimentos virtuais ou equivalentes, podemos utilizar coeficientes expressos em número de diâmetros da tubulação, uma vez que verifica-se uma relação entre o comprimento equivalente (Leq) das peças especiais e o diâmetro.
| Peça | Comprimento equivalente (x diâmetros) |
|---|---|
| Curva 90° | 30 |
| Curva 45° | 15 |
| Entrada normal | 16 |
| Entrada de borda | 35 |
| Registro de gaveta aberto | 8 |
| Registro de globo aberto | 350 |
| Saída de canalização | 35 |
| Tê passagem direta | 20 |
| Tê saída lateral | 50 |
| Tê saída bilateral | 65 |
| Válvula de retenção | 100 |
| Válvula de pé e crivo | 265 |
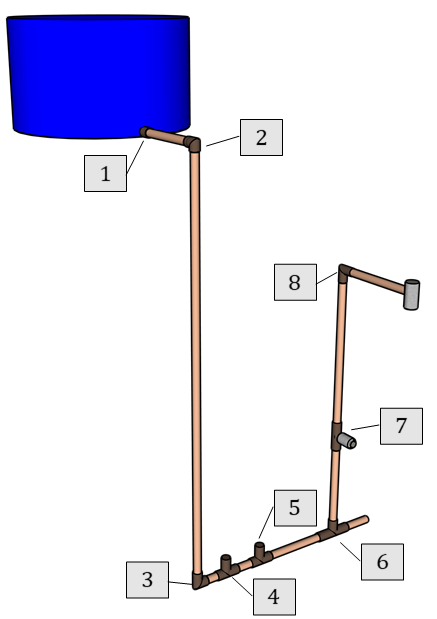
Exemplo 6.7 (Comprimento equivalente) Considere a instalação abaixo.
Calcular as perdas de carga para uma vazão do chuveiro de 4 L/min. Considerar a tubulação com 5 m de comprimento e diâmetro de 3/4”.
Solução.
Perda de carga contínua:
\(hf_{con} = \frac{6,107 \cdot 0,000135 \cdot (4/60000)^{1,75} \cdot 5}{0,019^{4,75}} = 0,0304 mca\)
Perda de carga localizada:
| Peça | L virtual (m) | |
|---|---|---|
| 1 | Entrada de canalização | 16 x 0,019 |
| 2 | Curva 90° | 30 x 0,019 |
| 3 | Curva 90° | 30 x 0,019 |
| 4 | Te passagem direta | 20 x 0,019 |
| 5 | Te passagem direta | 20 x 0,019 |
| 6 | Te saída lateral | 50 x 0,019 |
| 7 | Registro de gaveta | 8 x 0,019 |
| 8 | Curva 90° | 30 x 0,019 |
| TOTAL | 3,876 |
\(hf_{loc} = \frac{6,107 \cdot 0,000135 \cdot (4/60000)^{1,75} \cdot 3,876}{0,019^{4,75}} = 0,0234 mca\)
hft = hfloc + hf con
hft = 0,0304 + 0,0234 = 0,0538 mca