3.4 Vasos comunicantes
Pela equação da Lei de Stevin (Equação (3.3)), podemos concluir que a pressão exercida por um líquido não depende do volume ou do formato do recipiente em que está contido. A pressão hidrostática depende apenas da altura da coluna do fluido. Observando um líquido contido em recipientes interligados e abertos (Figura 3.3), cada um com volume e formato diferente, a altura deste líquido será igual em todos eles após o equilíbrio.

Figura 3.3: Vasos comunicantes. Observe que a altura do líquido é a mesma em todos os recipientes, independente do formato.
Fonte da imagem: O Autor
Quando dois líquidos imiscíveis são colocados em um tubo com formato de U, podemos aplicar a lei de Stevin para estabelecer uma relação de proporcionalidade entre as alturas das colunas de líquido e o peso específico de cada um. As alturas das colunas de líquido são proporcionais às densidades dos fluidos. Assim:
Pontos de mesma cota (altura) e no mesmo líquido estão sujeitos à mesma pressão.
Exemplo 3.2 (Vasos comunicantes) No esquema demonstrado na figura, calcule a pressão manométrica em todos os pontos do sistema.
- O líquido azul é água (D = 1,0).
- O líquido amarelo é óleo (D = 0,75).
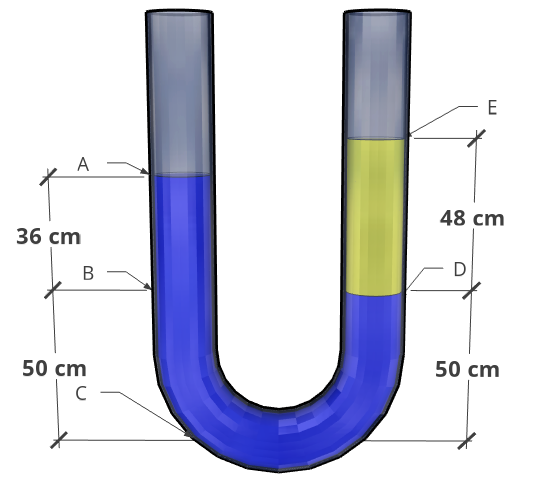
Fonte da imagem: O Autor
Solução.
\(P_A = P_{atm} = 0\)
\(P_B = 9810 N/m^3 \cdot 0,36 m = 3531,6 Pa\)
Para o ponto C, há duas maneira de calcular:
\(P_C = 9810 N/m^3 \cdot (0,36 + 0,50) m = 8436,6 Pa\)
\(P_C = (9810 \cdot 0,75) N/m-3 \cdot 0,48 m + 9810 N/m^3 \cdot 0,50 m = 8436,6 Pa\)
Ambos levam ao mesmo resultado.
\(P_D = (9810 \cdot 0,75) N/m^3 \cdot 0,48 m = 3531,6 Pa\)
PD é exatamente igual a PB.
\(P_E = P_{atm} = 0\)
Explicação detalhada no vídeo abaixo: