5.5 Orifício de grandes dimensões
Neste caso, não podemos admitir que todas as partículas possuem a mesma velocidade. Isso se deve ao fato de que a diferença na carga hidráulica em toda a área do orifício não pode ser desprezada. Logo, devemos usar a integral da equação (5.3) em função da altura “h”.
Para orifícios retangulares, a vazão é dada pela equação (5.4).
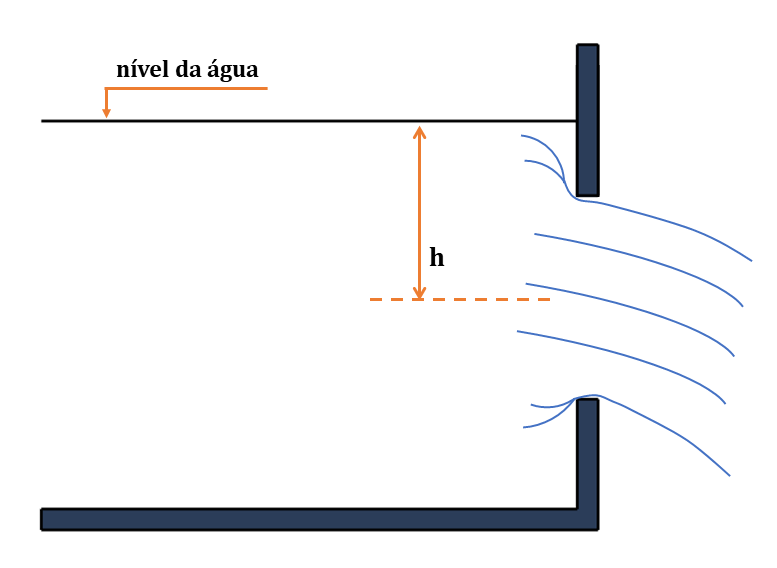
Figura 5.3: Representação de um orifício de grandes dimensões D > 1/10h
\[\begin{equation} Q = \frac{2}{3} \cdot Cd \cdot L \cdot \sqrt{2 \cdot g} \cdot (h_2^{3/2} - h_1^{3/2}) \tag{5.4} \end{equation}\]
em que:
- L é a largura do orifício.
- h1 é altura da água acima da base superior do orifício.
- h2 é altura da água acima da base inferior do orifício.
Exemplo 5.2 (Orifício grande) Um orifício retangular com 60 cm de altura e 75 cm de largura está instalado em um grande reservatório. A altura da água acima do centro do orifício é de 50 cm. Qual a vazão do orifício?
Solução.
\(Q = \frac{2}{3} \cdot 0,61 \cdot 0,75 \cdot \sqrt{19,62} \cdot (0,8^{3/2} - 0,2^{3/2}) = 0,85 m^3/s\)
Veja a resolução do exercício no vídeo abaixo: