4.4 Aplicações práticas do teorema de Bernoulli
O teorema de Bernoulli para fluidos perfeitos pode ser utilizado em lagumas situações práticas, em que as perdas de energia considerada são desprezíveis. É o caso do Tubo de Venturi e do Tubo de Pitot que serão estudados a seguir.
4.4.1 Tubo de Venturi
Consiste de uma seção convergente gradual, seguida de um estrangulamento (garganta) e de uma seção divergente gradual (Figura 4.1).
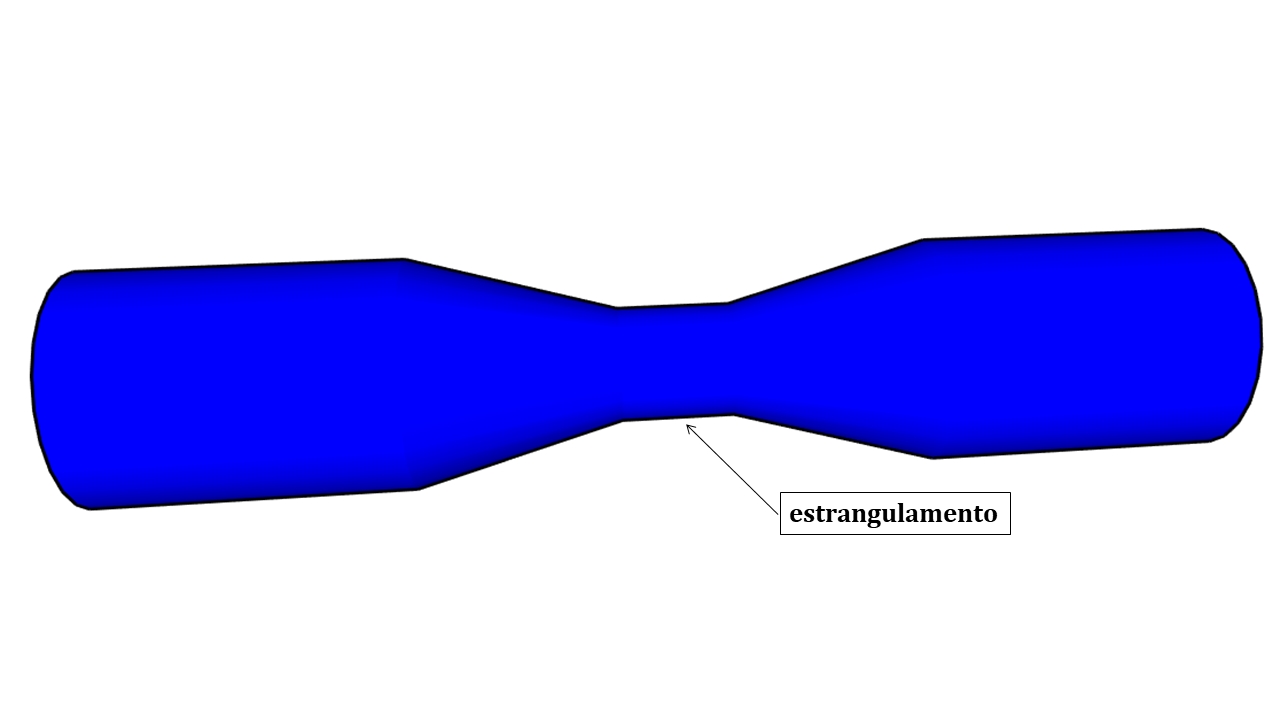
Figura 4.1: Representação esquemática de um Tubo de Venturi
No estrangulamento, observa-se uma diminuição da pressão devido ao aumento da velocidade, que pode ser comprovada pela aplicação do Teorema de Bernoulli (Eq. (4.4)). Este princípio se baseia na transformação de energia, em que parte da energia de pressão é transformada em energia cinética, quando passa pelo estrangulamento, e se transforma novamente em energia de pressão quando volta à tubulação principal.
Suas aplicações são variadas, como em carburadores de carros e aerógrafos para pintura, em que realiza a mistura de ar com combustível ou tinta. Na agricultura, é utilizado como injetor de fertilizantes (Figura 4.2) em fertirrigação e medidor de vazão em tubulações (Figura 4.3).
Para que funcione como um injetor de fertilizantes (Figura 4.2), é necessária uma vazão mínima na tubulação para que seja criada uma pressão negativa no estrangulamento. Dessa forma, a pressão atmosférica será responsável pela sucção da solução de fertilizante e mistura na água da tubulação.
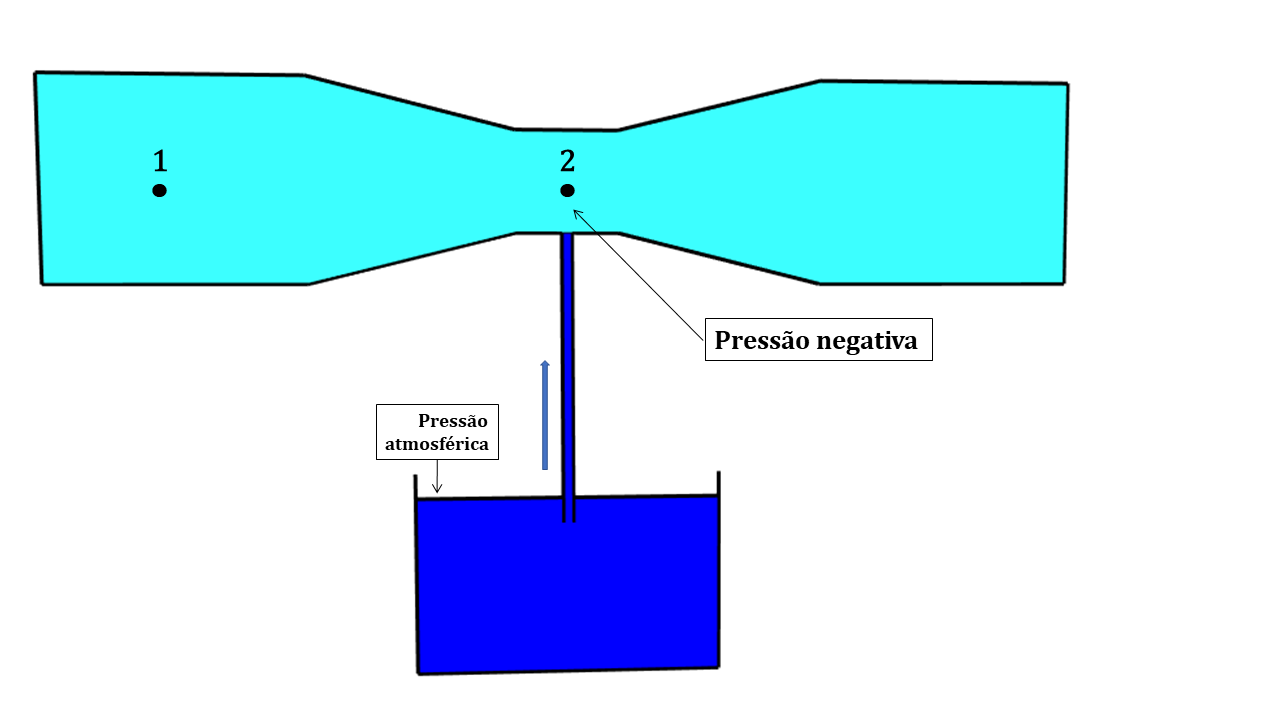
Figura 4.2: Representação esquemática de um Tubo de Venturi utilizado como injetor de fertilizantes na fertirrigação
Já para que o tubo de Venturi possa ser utilizado como um medidor de vazão (Figura 4.3), ele precisa trabalhar em conjunto com um medidor de pressão (manômetro). É preciso que se conheça a pressão no tubo antes do Venturi e a pressão no estrangulamento, ou apenas a diferença de pressão entre estes dois pontos. Na figura 4.3, o tubo de Venturi está ligado a um manômetro diferencial (Item 3.8.3). Outras configurações são possíveis, com piezômetros, manômetros metálicos, digitais, etc.
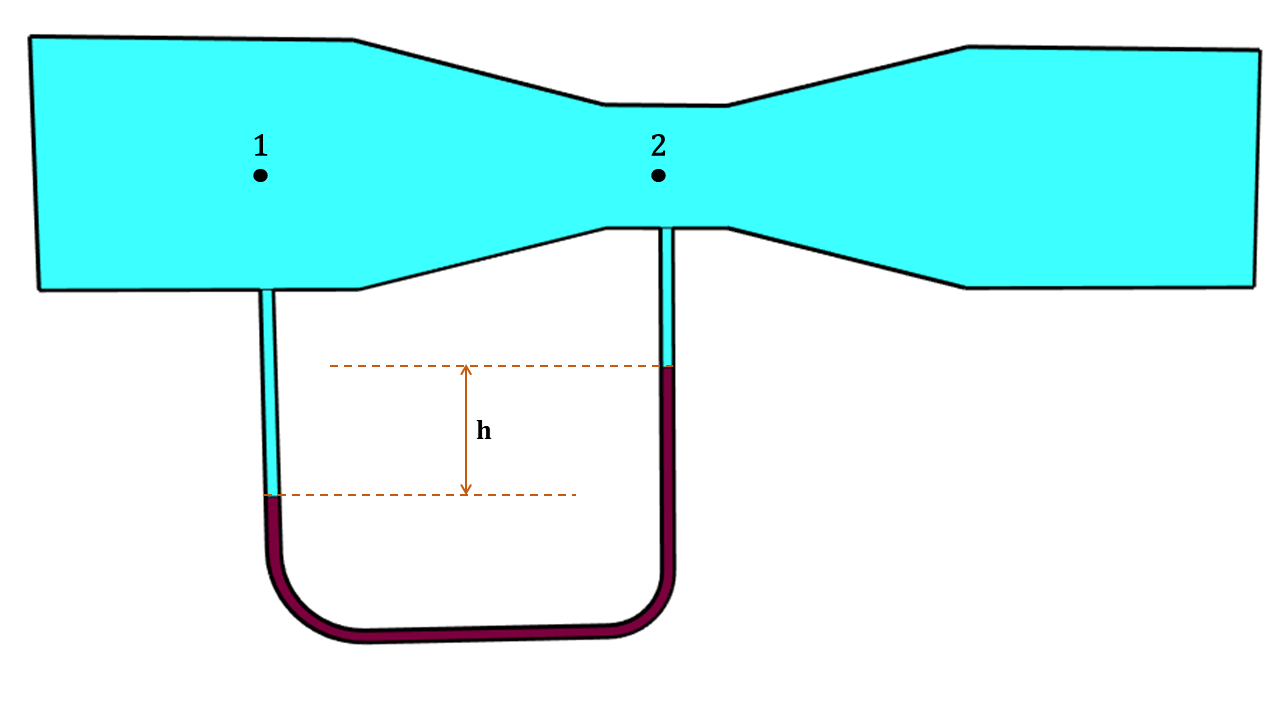
Figura 4.3: Representação esquemática de um Tubo de Venturi utilizado como medidor de vazão em tubulações
A vazão escoando pela tubulação é dada pela Equação (4.5).
\[\begin{equation} Q = \frac{\pi \cdot D_1^2} {4} \cdot \sqrt{\frac{2 \cdot g \cdot \Delta P}{ \left ( \frac{D_1}{D_2} \right ) ^ 4 - 1}} \tag{4.5} \end{equation}\]
Exemplo 4.7 (Vazão Venturi) Qual a vazão que escoa por uma tubulação de 50 mm de diâmetro em que está instalado um Venturi com 25 mm no estrangulamento. O sistema está ligado a um manômetro diferencial de mercúrio, cuja deflexão na coluna de mercúrio é de 45 cm.
Solução.
\(\Delta P = (13,6 - 1 ) \cdot 0,45 = 5,67 mca\)
\(Q = \frac{\pi \cdot 0,050^2} {4} \cdot \sqrt{\frac{19,62 \cdot 5,67}{ \left ( \frac{0,050}{0,025} \right ) ^ 4 - 1}} = 0,00537 m^3/s = 5,37 L/s\)
Veja no vídeo a seguir a solução explicada do exercício:
4.4.2 Tubo de Pitot
Consiste de dois tubos concêntricos de pequeno diâmetro. O tubo interno mede a energia total de escoamento, enquanto que o tubo externo mede unicamente a energia de pressão estática. A diferença entre o tubo interno e externo corresponde à carga cinética, ou seja, a energia de velocidade.
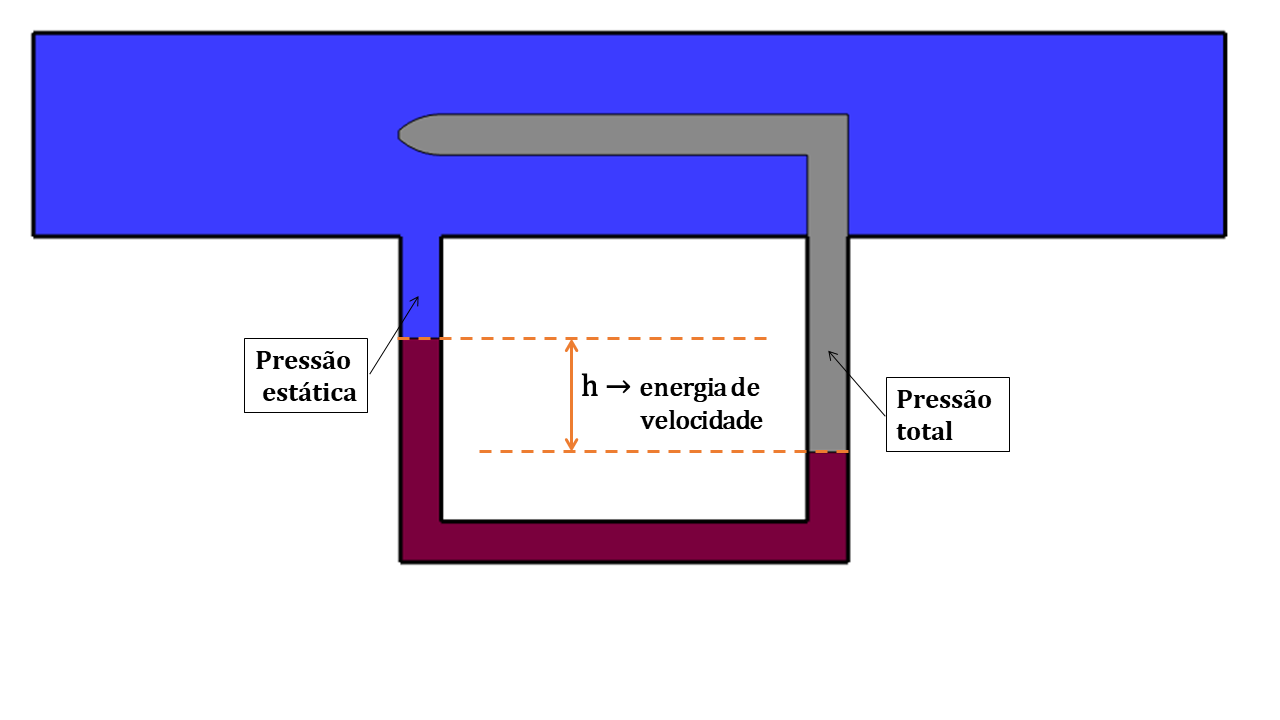
Figura 4.4: Representação esquemática de um Tubo de Pitot inserido em uma tubulação para medição da velocidade
Quando um tubo de Pitot é ligado a um manômetro diferencial, a velocidade da água escoando é calculada pela Equação (4.6). A vazão pode ser facilmente calculada combinando com a equação da vazão (Eq. (4.2)).
\[\begin{equation} V = \sqrt{ 2 \cdot g \cdot h \cdot ( D{man} - D{água})} \tag{4.6} \end{equation}\]
Tubos de Pitot são utilizados na aviação para medir a altitude e velocidade no ar dos aviões. Equipam desde pequenos monomotores até grandes jatos (Figura 4.5).

Figura 4.5: Tubo de Pitot em aviões: Cessna 172 Skyhawk II (acima) e Boeing 777-381 (abaixo)
O voo Air France 447
Em 31 de maio de 2009, o voo 447 da Air France que fazia a rota Rio de Janeiro - Paris caiu no Ocenao Atlântico com 228 pessoas a bordo.
O relatório final da investigação do acidente apontou que a tragédia foi causada por uma combinação de erros de avaliação dos pilotos devido a problemas técnicos ocorridos por congelamento nos sensores de velocidade (tubo de Pitot). Segundo o relatório as sondas Pitot, obstruídas por cristais de gelo, não conseguiram informar a velocidade correta da aeronave, o que causou a desconexão do piloto automático e em seguida diversos erros de avaliação dos pilotos.
Exemplo 4.8 (Pitot vazao) Um tubo de Pitot foi instalado no centro de uma tubulação de 200 mm de diâmetro que está conduzindo água. Se a deflexão da coluna de mercúrio é de 264 mm, calcular a vazão conduzida pela tubulação.
Solução.
\(V = \sqrt{ 19,62 \cdot 0,264 \cdot ( 13,6 - 1)} = 8,08 m/s\)
\(Q = \frac{\pi \cdot 0,200^2}{4} \cdot 8,08 = 0,25 m^3/s = 250 L/s\)
Veja a solução no vídeo a seguir: