8.3 Fórmula de Manning
É utilizada para dimensionamento de canais em escoamento permanente uniforme, sendo descrita como:
\(Q = \frac{1}{n}\cdot A\cdot RH^{2/3}\cdot i^{1/2}\)
em que
- Q – vazão, m3/s
- A – área molhada. m2
- RH - raio hidráulico, m
- i – declividade, m/m
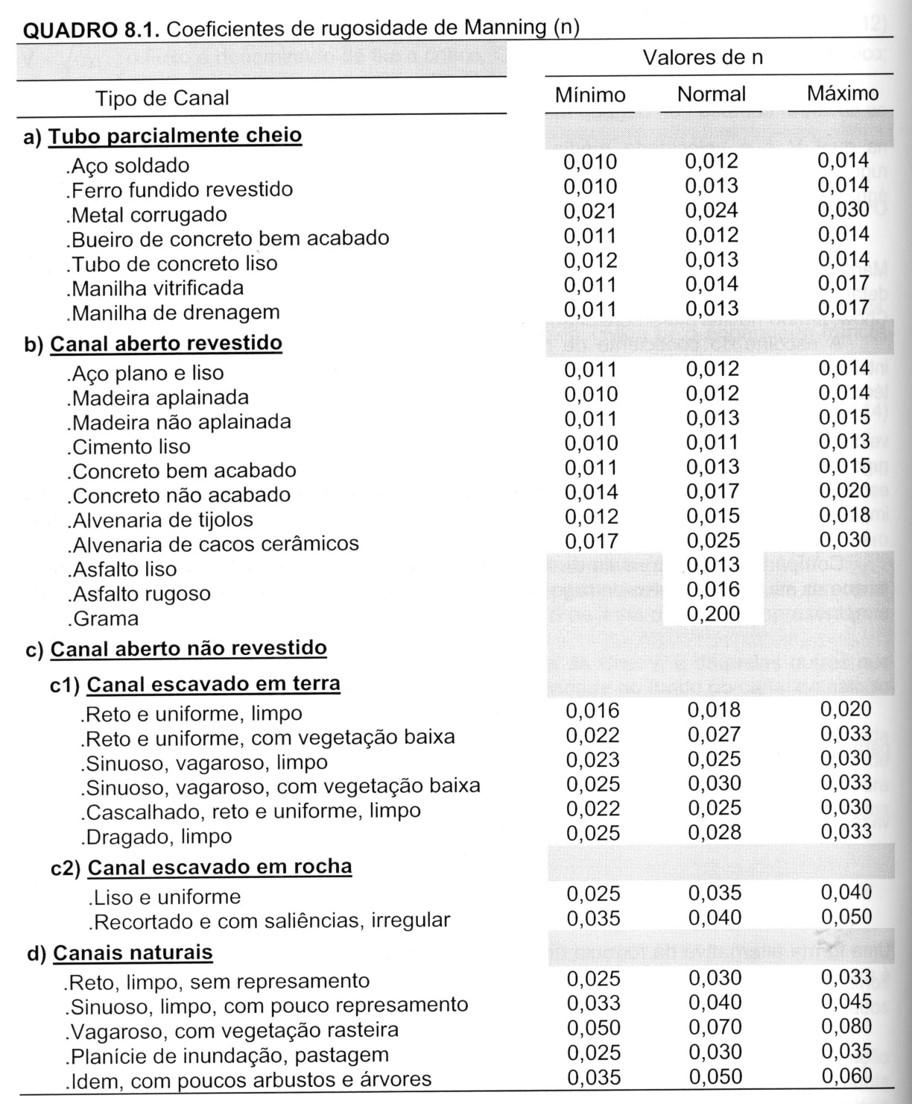
Figura 8.2: Coeficientes de rugosidade de Manning.
Exemplo 8.1 (Manning 1) Determinar a vazão de um canal trapezoidal com as seguintes características:
- Inclinação dos taludes: 1(vertical):1,5(horizontal)
- Declividade do canal: 1 m em 1500 m
- Largura do fundo (b): 3,5 m
- Profundidade de escoamento (y): 1,2 m
Considerar duas situações:
canal de paredes de terra reto, limpo e uniforme: n=0,018.
canal com paredes revestidas de concreto bem acabado: n=0,013.
Solução.
\(A = 1,2 \cdot (3,5 + 1,5 \cdot 1,2) = 6,36 m^2\)
\(P = 3,5 + 2 \cdot 1,2 \cdot \sqrt{1 + 1,5^2} = 7,83 m\)
\(RH = \frac{6,36}{7,,83} = 0,081 m\)
\(Q = \frac{1}{0,018} \cdot 6,36 \cdot 0,81^{2/3} \cdot (1/15000)^{1/2} = 7,93 m^3/s\)
\(Q = \frac{1}{0,013} \cdot 6,36 \cdot 0,81^{2/3} \cdot (1/15000)^{1/2} = 10,97 m^3/s\)
Exemplo 8.2 (Manning 2) Determinar a declividade que deve ser dada a um canal retangular para atender as seguintes condições de um projeto:
- Vazão (Q): 2,0 m3/s
- Profundidade de escoamento (y): 0,80 m
- Largura do fundo (b): 2,0 m
- Paredes revestidas de concreto bem acabado: n=0,013
Solução.
\(A = 0,8 \cdot 2 = 1,6 m^2\)
\(P = 2 + 2 \cdot 0,8 = 3,6 m\)
\(RH = \frac{1,6}{3,6} = 0,44 m\)
\(2 = \frac{1}{0,013} \cdot 1,6 \cdot 0,44^{2/3} \cdot i^{1/2} \rightarrow i = 0,000789 m/m\)
Exemplo 8.3 (Manning 3) Um canal escavado em terra com seção trapezoidal tem coeficiente de rugosidade n=0,020. Determinar sua profundidade de escoamento (y) para uma vazão (Q) de 6,5 m3/s, considerando-se as seguintes condições de projeto:
- Largura do fundo (b): 4,0 m
- Inclinação dos taludes: 1:1,5
- Declividade (i): 0,65%
Solução.
Atribuir um valor qualquer valor para a profundidade de escoamento, digamos, y=1,0 m e calcular a vazão:
\(A_{1,0} = 1,0 \cdot (4,0 + 1,5 \cdot 1,0) = 5,500 m^2\)
\(P_{1,0} = 4,0 + 2 \cdot 1,0 \cdot \sqrt{1 + 1,5^2} = 7,6061 m\)
\(RH_{1,0} = \frac{5,500}{7,61} = 0,723 m\)
\(Q_{1,0} = \frac{1}{0,020} \cdot 5,500 \cdot 0,723^{2/3} \cdot (0,65/100)^{1/2} = 17,863 m^3/s\)
A vazão ficou bem acima da requerida, diminuir o valor de y para, digamos, y=0,3 e recalcular a vazão:
\(A_{0,3} = 0,3 \cdot (4,0 + 1,5 \cdot 0,3) = 1,335 m^2\)
\(P_{0,3} = 4,0 + 2 \cdot 0,3 \cdot \sqrt{1 + 1,5^2} = 5,082 m\)
\(RH_{0,3} = \frac{5,56}{7,61} = 0,263 m\)
\(Q_{0,3} = \frac{1}{0,020} \cdot 1,335 \cdot 0,2633^{2/3} \cdot (0,65/100)^{1/2} = 2,207 m^3/s\)
Agora, a vazão ficou abaixo da requerida, aumentar o valor de y.
Prosseguir até chegar a uma vazão calculada bastante próxima da vazão requerida.
Para y = 0,564 m \(\rightarrow\) Q = 6,499 m3/s.
Logo, este valor de y = 0,564 m pode ser considerada a resposta correta.