7.1 Tubulações de sucção e recalque
A tubulação é denominada de sucção quando se localiza antes da motobomba, e de recalque quando se localiza depois da motobomba.
Na tubulação de sucção, geralmente se encontram as seguintes peças:
- Válvula de pé e crivo, só permite a passagem do líquido no sentido ascendente. Tem a função de manter a bomba escorvada e atua como filtro de impurezas.
- Curva de 90° devido ao traçado típico da tubulação.
- Redução que liga o final da tubulação de sucção à entrada da bomba, de diâmetro geralmente menor. Essa redução evita a formação de bolsas de ar na entrada da bomba
Na tubulação de recalque, geralmente encontramos as seguitnes peças:
- Ampliação concêntrica para ajuste do diâmetro.
- Válvula de retenção, unidirecional, que impede que o peso da coluna de água seja sustentado pela bomba, o que poderia desalinhá-la e impede o refluxo do líquido, fazendo a bomba funcionar como turbina, o que lhe provocaria danos.
- Válvula de gaveta com função de regular a vazão e permitir reparos no sistema.
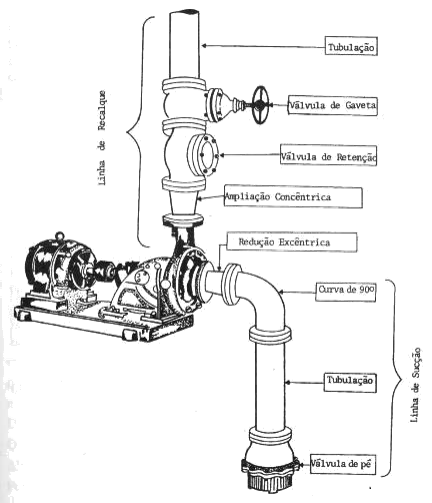
Figura 7.1: Configuração típica de uma estação de bombeamento.
7.1.1 Dimensionamento das tubulações de recalque e sucção
O dimensionamento das tubulações de recalque e sucção trata da seleção do material das tubulações, disposição das tubulações no projeto e, principalmente, na seleção do diâmetro adequado dstas tubulações.
Existem vários critérios para a escolha do diâmetro das tubulações. Um critério amplamente utilizado é baseado na velocidade máxima da água na tubulação. Para tubulações de recalque, podemos adotar a velocidade máxima de 2,0 m/s. Para tubulações de sucção, esta velocidade é menor, de 1,0 m/s.
No entanto, é possível adotar um critério mais completo para as tubulaões de recalque, que considera a velocidade mínima e máxima da água nas tubulações. Adotar uma velocidade mínima evita o depósito de sedimentos, enquanto que não ultrapassar a velocidade máxima evita danos estruturais às tubulações. Assim, podemos dimensionar a tubulação de forma que a velocidade fique entre 0,7 m/s e 5,0 m/s.
Assim:
\[\begin{equation} D_r=\sqrt{\frac{4 \cdot Q}{\pi \cdot (0,7 \leq V \leq 5,0)}} \tag{7.1} \end{equation}\]
e
\[\begin{equation} D_s=\sqrt{\frac{4 \cdot Q}{\pi \cdot 1,0}} \tag{7.2} \end{equation}\]
Os valores obtidos nas equações (7.1) e (7.2) devem ser utilizados para seleção dos diâmetros comerciais que mais se aproximem dos diâmetros calculados.
Exemplo 7.1 (Escolha do diâmetro) Para uma vazão de requerida no projeto de 6,8 m3/h, quais devem ser os diâmetros das tubulações de recalque e de sucção?
Solução.
\[ D_r=\sqrt{\frac{4 \cdot 6,8/3600}{\pi \cdot 5,0}} \cdot 1000 = 21,9 mm \]
\[ D_r=\sqrt{\frac{4 \cdot 6,8/3600}{\pi \cdot 0,7}} \cdot 1000 = 58,6 mm \]
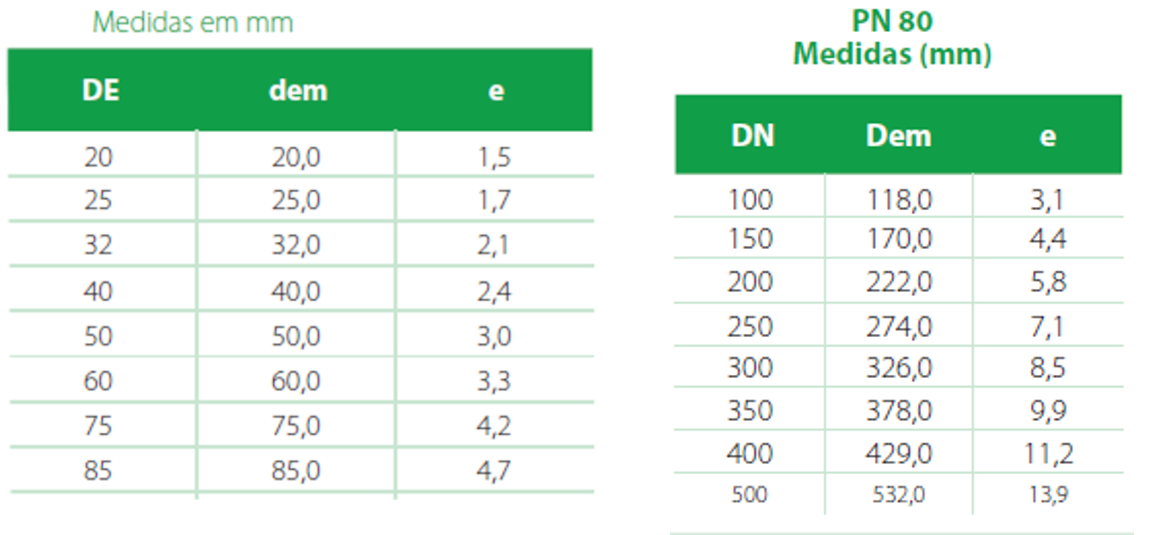
O diâmetro da tubulação de recalque deve ficar entre 21,9 mm e 58,6 mm. Analisando a tabela de diâmetros comerciais abaixo, (ver Figura 6.4), podemos escolher os diâmetros nominais entre 32 mm (Di = 27,8 mm) e 60 mm (Di = 53,4 mm).
\[ D_s=\sqrt{\frac{4 \cdot 6,8/3600}{\pi \cdot 1,0}} \cdot 1000 = 49,0 mm \]
Para a sucção, escolhemos o diâmetro nominal imediatamente acima do valor calculado, ou seja, o de 60 mm (Di = 53,4 mm).
| Diâmetro nominal | Diâmetro interno | |
|---|---|---|
| 1 | 32,00 | 27,80 |
| 2 | 40,00 | 35,20 |
| 3 | 50,00 | 44,00 |
| 4 | 60,00 | 53,40 |
O diâmetro da tubulação de sucção permanece inalterado (Dn=60mm, Di=53,4mm) para todas as opções.
7.1.2 Altura manométrica do sistema
Aplicando a equação do Teorema de Bernoulli, chegamos à conclusão que a altura manométrica de uma instalação é dada por:
\[\begin{equation} H_m = H_g + hf \tag{7.3} \end{equation}\]
em que:
- Hg- altura geométrica da instalação.
- hf - perdas de carga ocorridas na tubulação.
A altura geométrica é a diferença de altura entre o ponto mais baixo (captação) e o ponto mais alto (destino) do sistema.
As perdas de carga são aquelas de natureza contínua e localizada que ocorrem quando da movimentação da água pela tubulação.
Exemplo 7.2 (Altura manométrica.) Considere uma instalaçao de bombeamento com as seguintes características:
- Vazão requerida = 6,8 m3/h
- Comprimento da tubulação de recalque = 18 m
- Comprimento da tubulação de sucção = 1,0 m
- Altura geométrica de recalque = 3,0 m
- Altura geométrica de sucção - 1,0 m
- Material da tubulação: PVC
- Peças especiais no recalque:
- ampliação
- curva 90° (3x)
- válvula de retenção
- registro de gaveta
- Peças especiais na sucção:
- válvula de pé e crivo
- curva 90°
- redução
Calcule a altura manométrica da instalação.
Solução.
Perda de carga contínua no recalque:
\(hf_{cr} = \frac{6,107 \cdot 0,000135 \cdot (6,8/3600)^{1,75} \cdot 18}{0,0352^{4,75}} = 2,0357 mca\)
Perda de carga localizada no recalque:
| Peça especial | Coeficiente | Comprimento equivalente |
|---|---|---|
| Ampliação gradual | 10 | 0,40 |
| Válvula gaveta | 8 | 0,32 |
| Cotovelo 90° | 30 | 3,60 |
| Válvula de retenção | 100 | 4,00 |
| TOTAL | 8,32 |
\(hf_{lr} = \frac{6,107 \cdot 0,000135 \cdot (6,8/3600)^{1,75} \cdot 8,32}{0,0352^{4,75}} = 0,9410 mca\)
Perda de contínua na sucção:
\(hf_{cs} = \frac{10,643 \cdot (6,8/3600)^{1,852} \cdot 1}{140^{1,852} \cdot 0,0534^{4,871}} = 0,0161 mca\)
Perda de carga localizada na sucção
| Peça especial | Coeficiente | Comprimento equivalente |
|---|---|---|
| Redução excêntrica | 10 | 0,60 |
| Cotovelo 90° | 30 | 1,80 |
| Válvula de pé e crivo | 265 | 15,90 |
| TOTAL | 18,30 |
\(hf_{ls} = \frac{10,643 \cdot (6,8/3600)^{1,852} \cdot 18,30}{140^{1,852} \cdot 0,0534^{4,871}} = 0,2941 mca\)
Perda de carga total
\(hf = 2,0357 + 0,9410 + 0,0161 + 0,2941 = 3,2869 mca\)
Altura manométrica:
\(H_m = (3 + 1) + 3,2869 = 7,29 mca\)
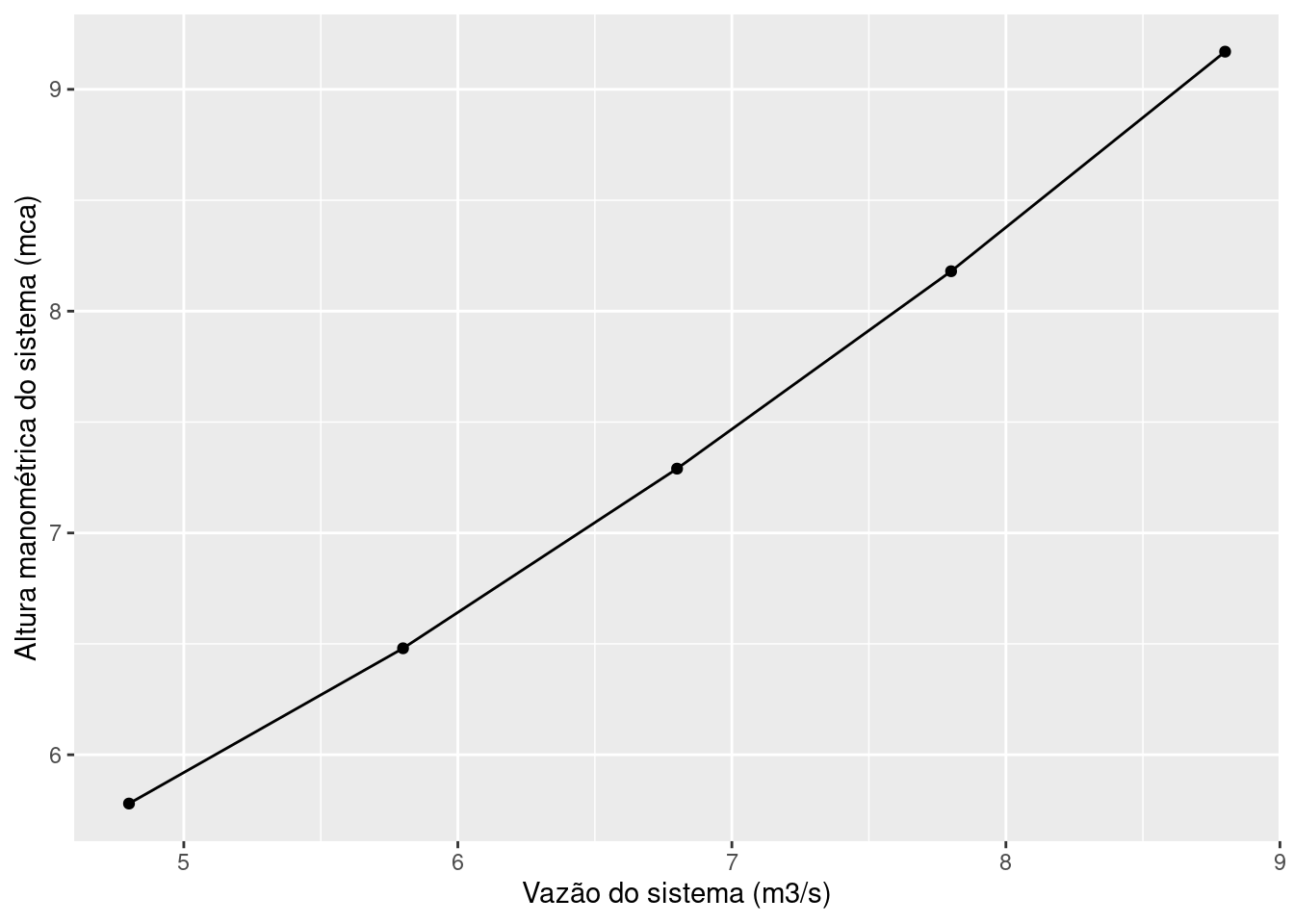
7.1.3 Curva característica do sistema
É uma relação entre a vazão recalcada e a altura manométrica do sistema correspondente. Deve ser plotada em forma de um gráfico, e utiliza-se pelo menos 5 valores de vazão (2 acima e 2 abaixo da vazão requerida).
Exemplo 7.3 Construa a curva característica do sistema do exemplo anterior.
Solução.
Utilizando 5 valores de vazão e calculando a respectiva altura manométrica para cada um, o resultado é:
| Q | Hm sistema |
|---|---|
| 4,80 | 5,78 |
| 5,80 | 6,48 |
| 6,80 | 7,29 |
| 7,80 | 8,18 |
| 8,80 | 9,17 |